Causal Inference and learning

I have started to learn more about the topic of causal inference and causal learning. Therefore, I have decided to put together here every resource I am using during my journey towards understanding this topic. My interest in this topic originated from the philosophical debate about causality, and recently, I have become interested in the current trends and attempt in the machine learning community for reconciling causal graphs with deep learning.

The Book of Why: The New Science of Cause and Effect

I think reading this book is the best starting point for understanding causality. The book is a combination of the technical report and popular science essay. It is very accessible and at the same time thought-provoking. Maybe it is a good idea, to begin reading this intreview and continue by reading the book.

ML beyond Curve Fitting: An Intro to Causal Inference and do-Calculus

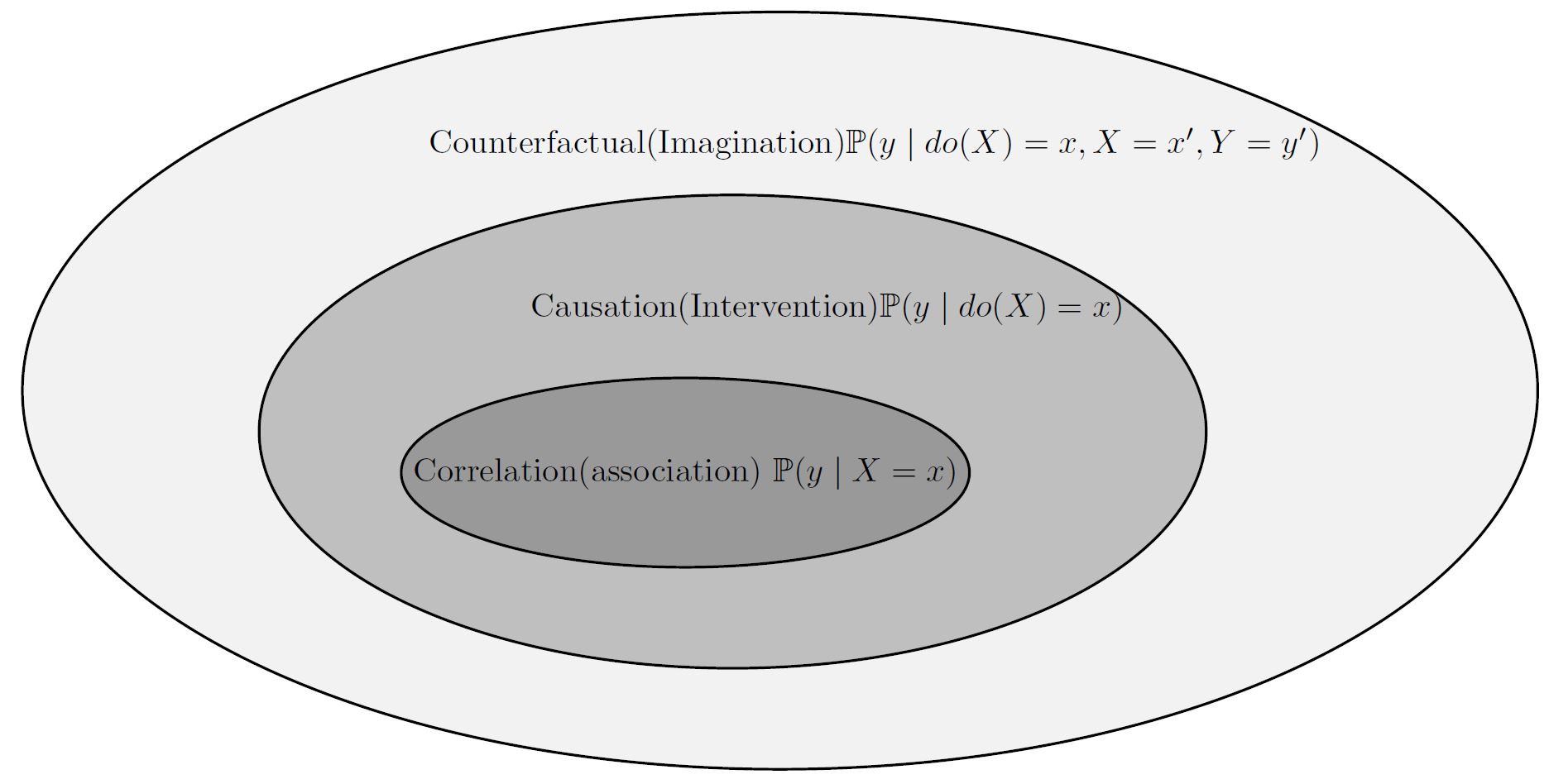
Ferenc Huszár did a nice job of putting together three tutorials on introducing causal inference and do-calculus. It covers the ladder of causation, from association and observation all the way towards intervention and counterfactuals. I found them very enjoyable reading. I definitely recommend reading this material.

• ML beyond Curve Fitting: An Intro to Causal Inference and do-Calculus
• Causal Inference 2: Illustrating Interventions via a Toy Example
• Causal Inference 3: Counterfactuals

Moreover, there are some videos that accompany this tutorial. Ferenc Huszár Causal Inference in Everyday Machine Learning

Constructing the world: Active causal learning in cognition

Although we are observing recent trends on reconciling causal inference with machine learning in the AI community, causality has been always one of the major topics in philosophy and psychology. There are a long-standing history and debate on causality and prominent philosophers such as David Hume have spent their career working in this subject. There is a debate about whether the world is causal or whether we are perceiving and understanding the world as causal. I believe that casualty is subjective and there is no such thing as the causal objective world. We are observing the world and inferring causal structure from observation and intervention; i.e., it is a good habit of the mind and can lead to scientific and technological discovery, and as a result, perceiving the world in this way has an evolutionary benefit.

Anyways, let us talk about this reference. Dr. Neil Bramley has done a great job of exploring active causal learning in cognition. How human interact with surrounding objects and choose appropriate intervention to unveil the causal structures. He has shown that interventional and temporal cues, along with top-down hierarchical constraints, inform the gradual evolution and adaptation of increasingly rich causal representations.

I recommend reading this Thesis to all the people who are interested in psychology and also reinforcement learning.

Mini course on causality, Cambridge MIT

This is the mini-course on causality presented by Jonas Peters. It contains more technical stuff and mathematical details. At first, I found it a little hard, but as time goes on, I was able to understand the material.

It has been divided into four different parts.

1. Part 1

It begins with an introduction to causal learning. Jonas presents some examples to show that Why causality matters and why we need to consider it seriously. Because most of the problem and decision making in real life consists of intervention and for being able to predict an outcome, we should equip ourselves with the tools of causal learning. After that, he introduces structural causal model (SCM) and shows how conditional distribution differs from interventional distribution.

Then he proceeds by introducing confounder, and how we can define a valid adjustment set. In the end, he explains how the randomized controlled experiment adjust for confounder variables.

1. Part 2

It starts by describing how we are identifying that two random variables, X and Y, are causally related, and how the causal strength is measured. Next, we will become familiar with one fundamental topic, instrumental variables, which has been important tools in economic studies. Then Jonas introduces one very important topics: counterfactuals. It is quite fundamental and widespread topic in philosophy and psychology. It is very related to imagination and retrospection. Moreover, it can be used to solve the problem of credit assignment and responsibility attribution. The goal of counterfactual is to answer a question like this: given the world we are living now, what would have happened if I had not attended to the university? This concept has significant implication in reinforcement learning, and we are observing more works. e.g., you can look at the following papers to learn more:

• Intrinsic Social Motivation via Causal Influence in Multi-Agent RL

• Designing agent incentives to avoid side effects

The summary of something we have discussed so far:

• Conditional distribution is different from interventional distribution.
• Given just observational distribution, we can not identify causal graph and therefore, we are not able to answer the question related to the intervention.
• Given the observational distribution and causal graph, we are equipped with sufficient knowledge to answer to the interventional query.
• SCM + observational distribution –> counterfactuals

Next, Jonas turns the topic and introduces the concept of d-separation in graphs. So far, we have just considered causal reasoning, i.e., having access to the structural causal model, we can answer questions about observation, intervention, and counterfactual. However, what will happen if we don’t know the causal graph and we have to construct it from scratch? That is the topic of causal learning or structure learning. In this setting, we have data, whether from observation or intervention, and the goal is to recover the causal graph and refine if after each observation. It is not possible always to recover causal graph, but by holding certain assumptions, it is possible to recover it within some certainty.

One method to approximately recover causal graph is independence-based methods. It is not possible to use this method without holding certain assumptions. Two assumptions that must be satisfied are:

• Markov property
• Faithfullness

Markov property: Given a DAG \(G\) and a joint distribution \(P_X\), this distribution is said to satisfy

• (i) the global Markov property with respect to the DAG G if:

  \[A; B\ d-sep.\ by\ C \rightarrow A \perp B \mid C\]

• (ii) the local Markov property with respect to the DAG G if each variable is independent of its non-descendants given its parents, and

• (iii) the Markov factorization property with respect to the DAG G if

Generally, when we have access to only observational data, we should take two steps to recover the causal graph.

• The first step is to learn independence and conditional independence between variables from observational data. When we are dealing with high-dimensional data, it can be a time-consuming and difficult task.

• Second, By inferring independence between variables and considering faithfulness assumption, we are able to recover causal graph up to some certainty.

The bad news is that even be holding Markov property, and faithfulness assumption, we are not able to recover causal graph completely. There can be different structures that satisfy independence and conditional independence properties. The class of structures which satisfy the same independence and conditional independence properties are called Markov equivalence.